Advertisements
Advertisements
प्रश्न
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
उत्तर
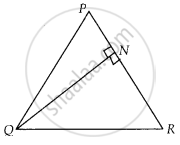
Given, ∆PQR,
N is a point on PR, such that QN ⊥ PR
And PN . NR = QN2
To prove: ∠PQR = 90°
Proof: We have, PN . NR = QN2
⇒ PN . NR = QN . QN
⇒ `("PN")/("QN") = ("QN")/("NR")` ...(i)
In ∆QNP and ∆RNQ,
`("PN")/("QN") = ("QN")/("NR")`
And ∠PNQ = ∠RNQ ...[Each equal to 90°]
∴ ∆QNP ~ ∆RNQ ...[By SAS similarity criterion]
Then, ∆QNP and ∆RNQ are equiangulars.
i.e., ∠PQN = ∠QRN
⇒ ∠RQN = ∠QPN
On adding both sides, we get
∠PQN + ∠RQN = ∠QRN + ∠QPN
⇒ ∠PQR = ∠QRN + ∠QPN ...(ii)
We know that, sum of angles of a triangle is 180°
In ∆PQR,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + ∠QPN + ∠QRN = 180° ...[∵ ∠QPR = ∠QPN and ∠QRP = ∠QRN]
⇒ ∠PQR + ∠PQR = 180° ...[Using equation (ii)]
⇒ 2∠PQR = 180°
⇒ ∠PQR = `180^circ/2` = 90°
∴ ∠PQR = 90°
Hence proved.
संबंधित प्रश्न
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
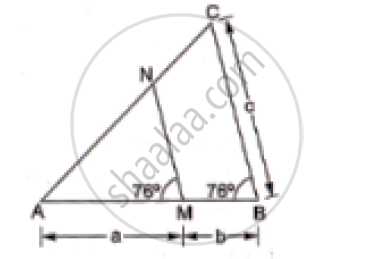
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
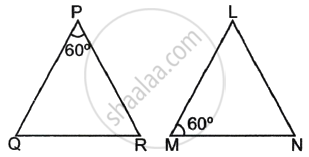
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
