Advertisements
Advertisements
प्रश्न
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
विकल्प
∠B = ∠E
∠A = ∠D
∠B = ∠D
∠A = ∠F
उत्तर
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ∠B = ∠D.
Explanation:
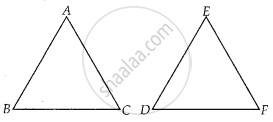
Given, in ∆ABC and ∆EDF,
`("AB")/("DE") = ("BC")/("FD")`
So, ∆ABC ~ ∆EDF if ∠B = ∠D ...[By SAS similarity criterion]
संबंधित प्रश्न
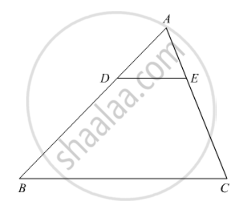
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC.
State the two properties which are necessary for given two triangles to be similar.
In the given figure MN|| BC and AM: MB= 1: 2
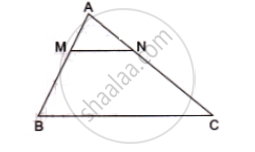
find ` (area(ΔAMN))/(area(ΔABC))`
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).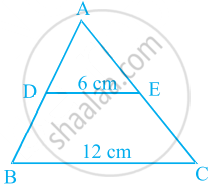
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
