Advertisements
Advertisements
प्रश्न
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).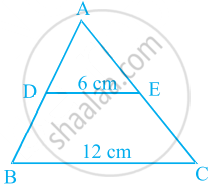
उत्तर
Given,
DE || BC,
DE = 6 cm
And BC = 12 cm
In ΔABC and ΔADE,
∠ABC = ∠ADE ...[Corresponding angle]
∠ACB = ∠AED ...[Corresponding angle]
And ∠A = ∠A ...[Common side]
∴ ΔABC ∼ ΔAED ...[By AAA similarity criterion]
Then, `("ar(ΔADE)")/("ar(ΔABC)") = ("DE")^2/("BC")^2`
= `(6)^2/(12)^2`
= `(1/2)^2`
⇒ `("ar(ΔADE)")/("ar(ΔABC)") = (1/2)^2 = 1/4`
Let ar(ΔADE) = k,
Then ar(ΔABC) = 4k
Now, ar(DECB) = ar(ABC) – ar(ΔADE)
= 4k – k
= 3k
∴ Required ratio = ar(ADE) : ar(DECB)
= k : 3k
= 1 : 3
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In the given figure, value of x(in cm) is

In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?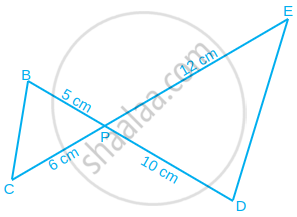
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
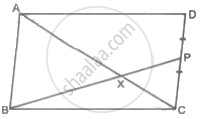
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

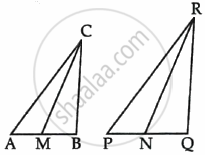
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.