Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
उत्तर
Given, a trapezium ABCD in which AB || DC.
P and Q are points on AD and BC, respectively such that PQ || DC.
Thus, AB || PQ || DC.
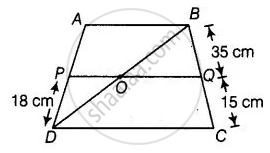
Join BD.
In ΔABD,
PO || AB ...[∵ PQ || AB]
By basic proportionality theorem,
`("DP")/("AP") = ("DO")/("OB")` ...(i)
In ΔBDC,
OQ || DC ...[∵ PQ || DC]
By basic proportionality theorem,
`("BQ")/("QC") = ("OB")/("OD")`
⇒ `("QC")/("BQ") = ("OD")/("OB")` ...(ii)
From equation (i) and (ii),
`("DP")/("AP") = ("QC")/("BQ")`
⇒ `18/("AP") = 15/35`
⇒ AP = `(18 xx 35)/15` = 42
∴ AD = AP + DP
= 42 + 18
= 60 cm
APPEARS IN
संबंधित प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
In a ABC , AD is a median and AL ⊥ BC .
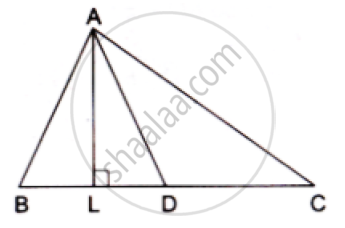
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

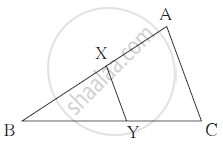
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
State and prove Basic Proportionality theorem.
