Advertisements
Advertisements
Question
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Solution
Given, a trapezium ABCD in which AB || DC.
P and Q are points on AD and BC, respectively such that PQ || DC.
Thus, AB || PQ || DC.
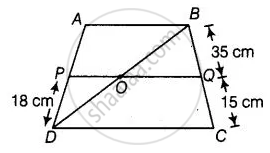
Join BD.
In ΔABD,
PO || AB ...[∵ PQ || AB]
By basic proportionality theorem,
`("DP")/("AP") = ("DO")/("OB")` ...(i)
In ΔBDC,
OQ || DC ...[∵ PQ || DC]
By basic proportionality theorem,
`("BQ")/("QC") = ("OB")/("OD")`
⇒ `("QC")/("BQ") = ("OD")/("OB")` ...(ii)
From equation (i) and (ii),
`("DP")/("AP") = ("QC")/("BQ")`
⇒ `18/("AP") = 15/35`
⇒ AP = `(18 xx 35)/15` = 42
∴ AD = AP + DP
= 42 + 18
= 60 cm
APPEARS IN
RELATED QUESTIONS
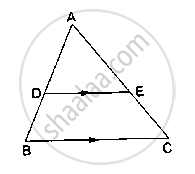
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
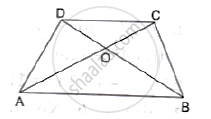
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
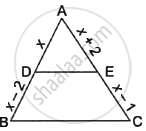
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.