Advertisements
Advertisements
Question
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Solution
Let ABCD be the rhombus with diagonals (AC = 24 cm and BD = 10 cm) meeting at O.
We know that the diagonals of a rhombus bisect each other at angles.
Applying Pythagoras theorem in right-angled AOB, we get:
`AB^2=AO^2+BO^2=12^2+5^2`
`AB^2=144+25=169`
`AB=sqrt169=13 cm`
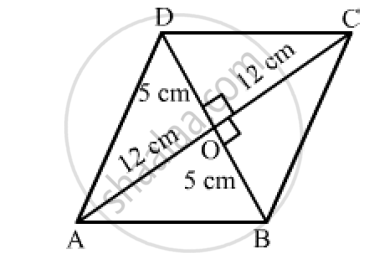
Hence, the length of each side of the rhombus is 13 cm.
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
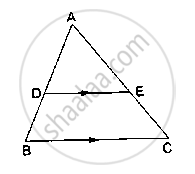
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
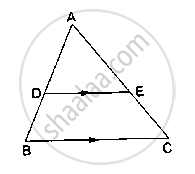
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
Find the height of an equilateral triangle of side 12cm.
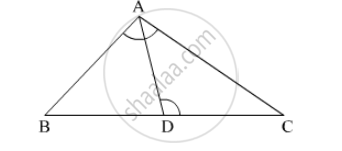
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
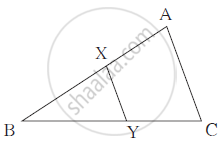
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.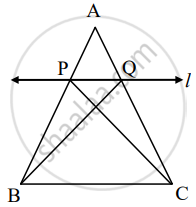
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
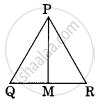
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
