Advertisements
Advertisements
Question
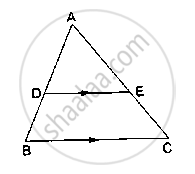
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
Solution
In Δ ABC, it is given that DE ∥ BC.
Applying Thales’ theorem, we get:
`(AD)/(DB) = (AE)/(EC)`
∵ AD = 3.6 cm , AB = 10 cm, AE = 4.5cm
∴ DB = 10 − 3.6 = 6.4cm
Or,`(3. 6) /(6.4)=(4.5)/(EC)`
Or, EC =`(6. 4× 4.5)/3.6`
Or, EC= 8 cm
Thus, AC = AE + EC
= 4.5 + 8 = 12.5 cm
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
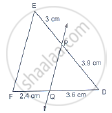
In below Fig., state if PQ || EF.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Find the height of an equilateral triangle of side 12cm.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
