Advertisements
Advertisements
Question
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
Solution

Let A be the first aeroplane flied due north at a speed of 1000 km/hr and B be the second aeroplane flied due west at a speed of 1200 km/hr
Distance covered by plane A in` 1 1/2 hours=1000xx3/2=1500km`
Distance covered by plane B in `1 1/2 hours = 1200xx3/2=1800 km`
Now, In right triangle ABC
By using Pythagoras theorem, we have
`AB^2=BC^2+CA^2`
=(1800)^2+(1500)^2
=3240000+2250000
=5490000
∴ `AB^2=5490000 `
⇒` AB=300sqrt61m`
Hence, the distance between two planes after `1 1/2 house is 300 sqrt61m`
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
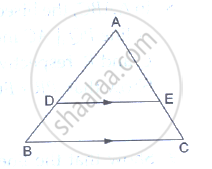
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
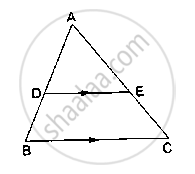
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
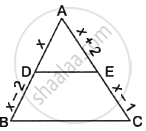
State and prove Basic Proportionality theorem.
