Advertisements
Advertisements
Question
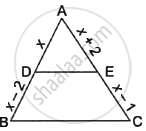
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
Solution
In ΔABC, DE||BC
∴ `(AD)/(DB) = (AE)/(EC)` ...(By basic proportionality theorem)
`\implies x/(x - 2) = (x + 2)/(x - 1)`
`\implies` x(x – 1) = (x + 2) (x – 2)
`\implies` x2 – x = x2 – 4
`\implies` –x = –4
`\implies` x = 4
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
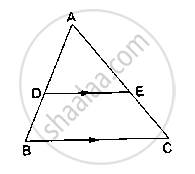
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
