Advertisements
Advertisements
प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
उत्तर

Let A be the first aeroplane flied due north at a speed of 1000 km/hr and B be the second aeroplane flied due west at a speed of 1200 km/hr
Distance covered by plane A in` 1 1/2 hours=1000xx3/2=1500km`
Distance covered by plane B in `1 1/2 hours = 1200xx3/2=1800 km`
Now, In right triangle ABC
By using Pythagoras theorem, we have
`AB^2=BC^2+CA^2`
=(1800)^2+(1500)^2
=3240000+2250000
=5490000
∴ `AB^2=5490000 `
⇒` AB=300sqrt61m`
Hence, the distance between two planes after `1 1/2 house is 300 sqrt61m`
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
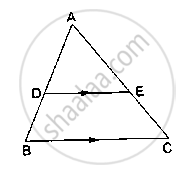
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
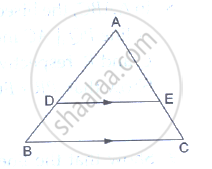
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
Find the height of an equilateral triangle of side 12cm.
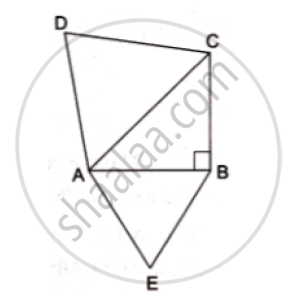
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
