Advertisements
Advertisements
प्रश्न
Find the height of an equilateral triangle of side 12cm.
उत्तर
Let ABC be the equilateral triangle with AD as an altitude from A meeting BC at D. Then, D will be the midpoint of BC.
Applying Pythagoras theorem in right-angled triangle ABD, we get:

`AB^2=AD^2+BD^2`
`⇒ AD^2=12^2-6^2(∵BD=1/2 BC=6)`
`⇒AD^2=144-36=108`
`⇒AD=sqrt108=6sqrt3 cm`
Hence, the height of the given triangle is `6sqrt3` cm.
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
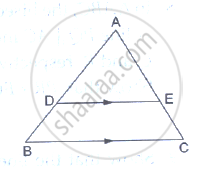
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
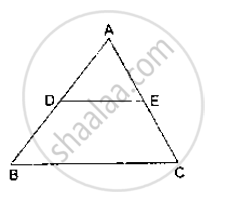
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

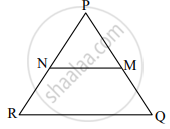
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
