Advertisements
Advertisements
प्रश्न
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
उत्तर
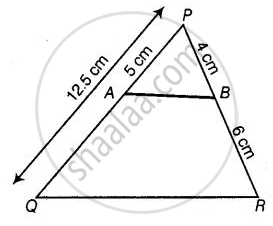
Given,
PQ = 12.5 cm,
PA = 5 cm,
BR = 6 cm
And PB = 4 cm
Then, QA = QP – PA
= 12.5 – 5
= 7.5 cm
Now, `("PA")/("AQ")`
= `5/7.5`
= `50/75`
= `2/3` ...(i)
And `("PB")/("BR")`
= `4/6`
= `2/3` ...(ii)
From equations (i) and (ii),
`("PA")/("AQ") = ("PB")/("BR")`
By converse of basic proportionally theorem,
AB || QR
APPEARS IN
संबंधित प्रश्न
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
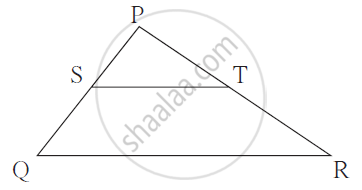
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
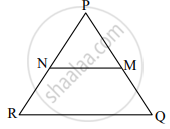
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
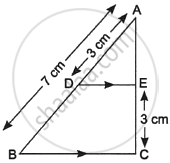
State and prove Basic Proportionality theorem.
