Advertisements
Advertisements
प्रश्न
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
उत्तर
Draw AE⊥BC, meeting BC at D.
Applying Pythagoras theorem in right-angled triangle AED, we get:
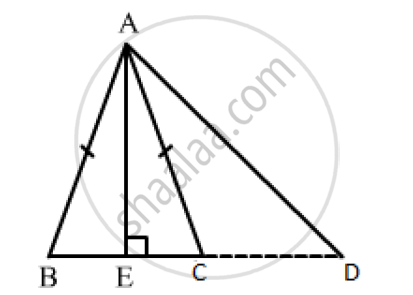
Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.
So, BE = CE
And DE+CE=DE+BE=BD
`AD^2=AE^2+DE^2`
`⇒ AE^2=AD^2-DE^2 ` ...............(1)
In ΔACE,
`AC^2=AE^2+EC^2`
⇒ `AE^2=AC^2-EC^2 ` ...............(2)
Using (i) and (ii),
⇒` AD^2-DE^2=AC^2-EC^2`
⇒` AD^2-AC^2=DE^2-EC^2`
`=(DE+CE) (DE-CE)`
`(DE+BE) CD`
`BD.CD`
APPEARS IN
संबंधित प्रश्न
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
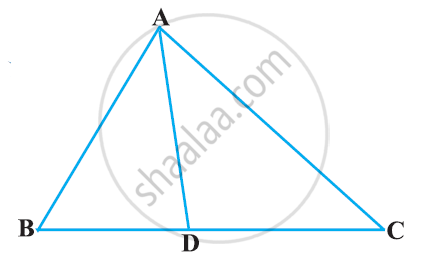
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

State the basic proportionality theorem.
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

