Advertisements
Advertisements
प्रश्न
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

उत्तर
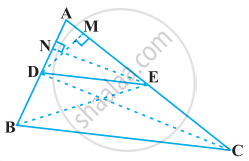
Proof: We are given a triangle ABC in which a line parallel to side BC intersects the other two sides AB and AC at D and E respectively.
We need to prove that `(AD)/(DB) = (AE)/(EC)`
Let us join BE and CD and then draw DM ⊥ AC and EN ⊥ AB.
Now, area of ∆ADE = `1/2` (base × height) = `1/2` AD × EN
The area of ∆ADE is denoted as ar(ADE).
So, ar(ADE) = `1/2` AD × EN
Similarly, ar(BDE) = `1/2` DB × EN,
ar(ADE) = `1/2` AE × DM and ar(DEC) = `1/2` EC × DM
Therefore, `(ar(ADE))/(ar(BDE)) = (1/2 AD xx EN)/(1/2 DB xx EN) = (AD)/(DB)` ......(1)
And `(ar(ADE))/(ar(DEC)) = (1/2 AE xx DM)/(1/2 EC xx DM) = (AE)/(EC)` ......(2)
Note that ∆BDE and DEC are on the same base DE and between the same parallels BC and DE.
So, ar(BDE) = ar(DEC) ......(3)
Therefore, from (1), (2) and (3), we have:
`(AD)/(DB) = (AE)/(EC)`
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Find the height of an equilateral triangle of side 12cm.
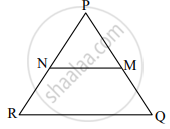
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
