Advertisements
Advertisements
प्रश्न
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
उत्तर
Given, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm
Also, PA, QB, RC and SD are all perpendiculars to line l
∴ PA || QB || RC || SD
By basic proportionality theorem,
PQ : QR : RS = AB : BC : CD
= 6 : 9 : 12
Let PQ = 6x, QR = 9x and RS = 12x
Since, length of PS = 36 cm
∴ PQ + QR + RS = 36
⇒ 6x + 9x + 12x = 36
⇒ 27x = 36
∴ x = `36/27 = 4/3`
Now, PQ = 6x
= `6 xx 4/3`
= 8 cm
QR = 9x
= `9 xx 4/3`
= 12 cm
And RS = 12x
= `12 xx 4/3`
= 16 cm
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
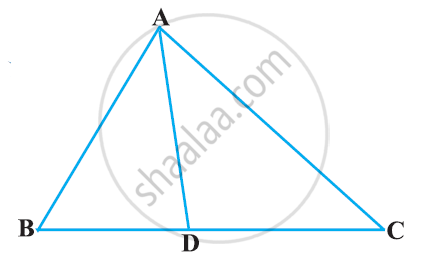
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the height of an equilateral triangle of side 12cm.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

State and prove Basic Proportionality theorem.
