Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
उत्तर
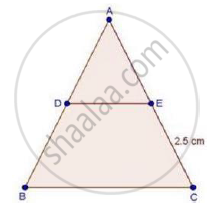
We have, DE || BC
Therefore, by basic proportionality theorem,
We have,
`"AD"/"BD"="AE"/"EC"`
`rArr4/5="AE"/2.5`
`rArr"AE"=(4xx2.5)/5`
⇒ AE = 2 cm
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
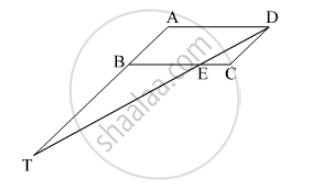
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.
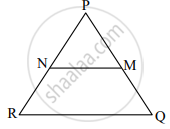
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
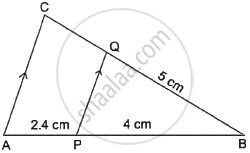
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.