Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
उत्तर
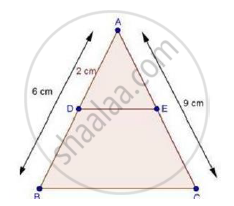
We have,
AD = 2 cm, AB = 6 cm
∴ DB = AB – AD
= 6 – 2
⇒ DB = 4 cm
And, DE || BC
Therefore, by basic proportionality theorem, we have,
`"AD"/"DB"="AE"/"EC"`
Taking reciprocal on both sides, we get,
`"DB"/"AD"="EC"/"AE"`
`4/2="EC"/"AE"`
Adding 1 on both sides, we get
`4/2+1="EC"/"AE"+1`
`rArr(4+2)/2=("EC"+"AE")/"AE"`
`rArr6/2="AC"/"AE"` [∵ EC + AE = AC]
`rArr6/2=9/"AE"` [∵ AC = 9cm]
`"AE"=(9xx2)/6`
⇒ AE = 3 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
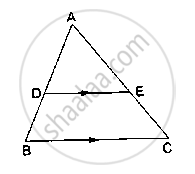
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
State the midpoint theorem
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
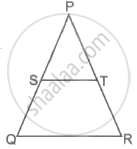
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.