Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
उत्तर
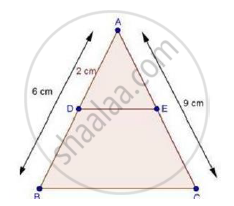
We have,
AD = 2 cm, AB = 6 cm
∴ DB = AB – AD
= 6 – 2
⇒ DB = 4 cm
And, DE || BC
Therefore, by basic proportionality theorem, we have,
`"AD"/"DB"="AE"/"EC"`
Taking reciprocal on both sides, we get,
`"DB"/"AD"="EC"/"AE"`
`4/2="EC"/"AE"`
Adding 1 on both sides, we get
`4/2+1="EC"/"AE"+1`
`rArr(4+2)/2=("EC"+"AE")/"AE"`
`rArr6/2="AC"/"AE"` [∵ EC + AE = AC]
`rArr6/2=9/"AE"` [∵ AC = 9cm]
`"AE"=(9xx2)/6`
⇒ AE = 3 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
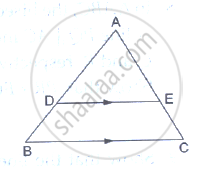
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In fig, seg DE || sec BC, identify the correct statement.

From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
