Advertisements
Advertisements
प्रश्न
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
उत्तर
In isosceles Δ ABC, we have:
AB = AC = 2a units and BC = a units
Let AD be the altitude drawn from A that meets BC at D.
Then, D is the midpoint of BC.
`BD=BC=a/2` units
Applying Pythagoras theorem in right-angled ΔABD, we have:
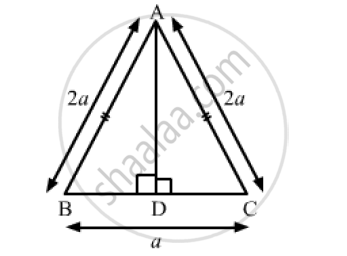
`AB^2=AD^2+BD^2`
`AD^2=AB^2-BD^2=(2a)^2-(a/2)^2`
`AD^2=4a^2-a^2/4=(15a^2)/4`
`AD= sqrt((15a^2)/4
)= (asqrt15)/2` unit
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
Find the height of an equilateral triangle of side 12cm.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
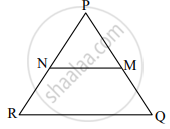
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

