Advertisements
Advertisements
प्रश्न
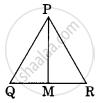
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
उत्तर
In isosceles Δ ABC, we have:
AB = AC = 2a units and BC = a units
Let AD be the altitude drawn from A that meets BC at D.
Then, D is the midpoint of BC.
`BD=BC=a/2` units
Applying Pythagoras theorem in right-angled ΔABD, we have:
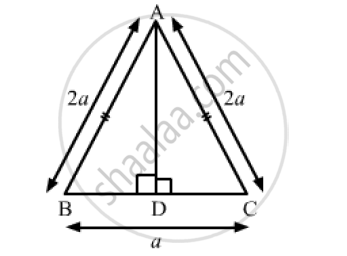
`AB^2=AD^2+BD^2`
`AD^2=AB^2-BD^2=(2a)^2-(a/2)^2`
`AD^2=4a^2-a^2/4=(15a^2)/4`
`AD= sqrt((15a^2)/4
)= (asqrt15)/2` unit
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
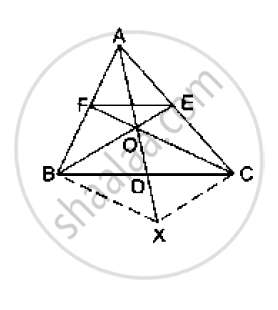
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`