Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
उत्तर
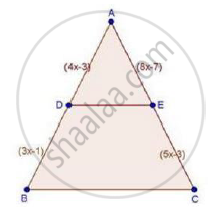
We have,
DE || BC
Therefore, by basic proportionality theorem, we have,
`"AD"/"DB"="AE"/"EC"`
`rArr(8x-7)/(5x-3)=(4x-3)/(3x-1)`
⇒ (8x − 7)(3x − 1) = (4x − 3)(5x − 3)
⇒ 24x2 − 8x − 21x + 7 = 20x2 − 12x − 15x + 9
⇒ 24x2 − 20x2 − 29x + 27x + 7 − 9 = 0
⇒ 4x2 − 2x − 2 = 0
⇒ 2[2x2 − x − 1] = 0
⇒ 2x2 − x − 1 = 0
⇒ 2x2 − 2x + 1x − 1 = 0
⇒ 2x(x − 1) + 1(x − 1) = 0
⇒ (2x + 1) (x – 1) = 0
⇒ 2x + 1 = 0 or x – 1 = 0
⇒ x = −1/2 or x = 1
𝑥 = −1/2 is not possible
∴ x = 1
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
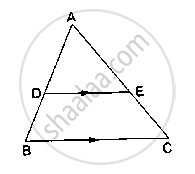
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
In below Fig., state if PQ || EF.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
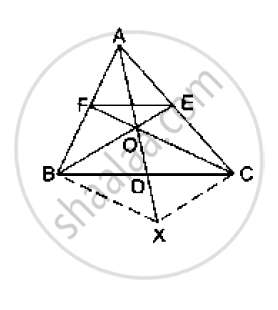
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

State and converse of Thale’s theorem.
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
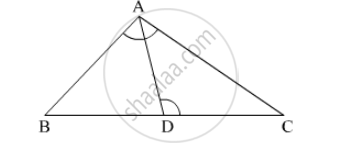
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
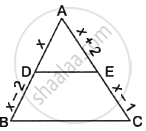
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
Find the value of x for which DE || AB in figure.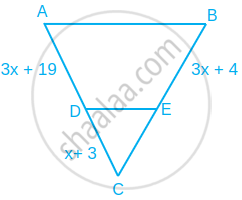
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

