Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
उत्तर
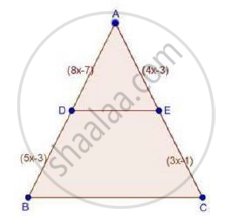
We have,
DE || BC
Therefore, by basic proportionality theorem,
We have,
`"AD"/"DB"="AE"/"EC"`
`rArrx/(x-2)=(x+2)/(x-1)`
⇒ x(x − 1) = (x + 2)(x − 2)
⇒ x2 − x = x2 − (2)2 [∵ (a – b) (a + b) = a2 − b2]
⇒ −x = −4
⇒ x = 4 cm
∴ x = 4 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
In a ABC , AD is a median and AL ⊥ BC .
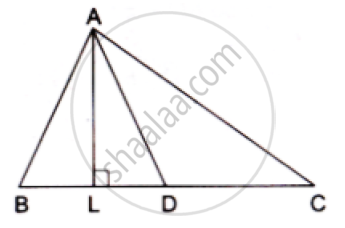
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
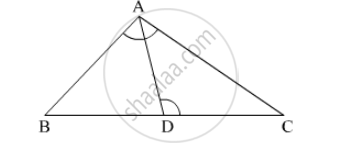
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
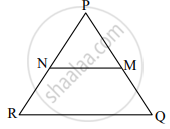
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
State and prove Basic Proportionality theorem.
