Advertisements
Advertisements
प्रश्न
State and prove Basic Proportionality theorem.
उत्तर
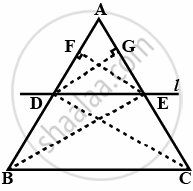
Basic Proportionality Theorem states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides of the triangle in proportion.
Let ABC be the triangle.
The line 1 parallel to BC intersect AB at D and AC at E.
To prove `(AD)/(DB) = (AE)/(EC)`
Join BE, CD
Draw EF ⊥ AB, DG ⊥ CA
Since EF ⊥ AB,
EF is the height of triangles ADE and DBE
Area of ΔADE = `1/2 xx "base" xx "height"`
= `1/2 AD xx EF`
Area of ΔDBE = `1/2 xx DB xx EF`
`("Area of" ΔADE)/("Area of" ΔDBE) = (1/2 xx AD xx EF)/(1/2 xx DB xx EF) = (AD)/(DB)` ...(1)
Similarly,
`("Area of" ΔADE)/("Area of" ΔDCE) = (1/2 xx AE xx DG)/(1/2 xx EC xx DG) = (AE)/(EC)` ...(2)
But ΔDBE and ΔDCE are the same base DE and between the same parallel straight line BC and DE.
Area of ΔDBE = Area of ΔDCE ...(3)
From (1), (2) and (3), we have
`(AD)/(DB) = (AE)/(EC)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In below Fig., state if PQ || EF.
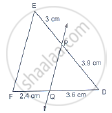
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

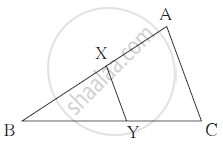
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

