Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
उत्तर
In Δ ABC, it is given that DE || BC.
Applying Thales’ theorem, we have :
`(AD)/(DB) = (AE)/(EC)`
⟹ `(7x - 4)/(3x +4) = (5x -2)/(3x)`
⟹ 3x (7x-4) = (5x-2) (3x+4)
⟹ `21x^2 – 12x = 15x^2 + 14x-8`
⟹ `6𝑥^2 – 26x + 8 = 0`
⟹ (x-4) (6x-2) =0
⟹ `x = 4,1/2`
∵ `x ≠ 1/3` (as if x = `1/3` 𝑡ℎ𝑒𝑛 𝐴𝐸 𝑤𝑖𝑙𝑙 𝑏𝑒𝑐𝑜𝑚𝑒 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑒)
∴ x = 4 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
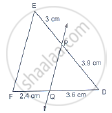
In below Fig., state if PQ || EF.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
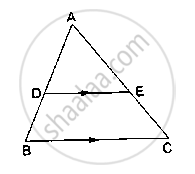
State and converse of Thale’s theorem.
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
Find the value of x for which DE || AB in figure.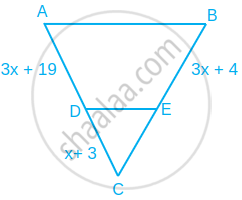
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`
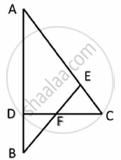
State and prove Basic Proportionality theorem.
