Advertisements
Advertisements
प्रश्न
Find the value of x for which DE || AB in figure.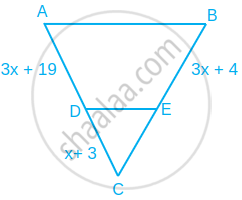
उत्तर
According to the question,
DE || AB
Using basic proportionality theorem,
`("CD")/("AD") = ("CE")/("BE")`
∴ If a line is drawn parallel to one side of a triangle such that it intersects the other sides at distinct points, then, the other two sides are divided in the same ratio.
Hence, we can conclude that, the line drawn is equal to the third side of the triangle.
⇒ `(x + 3)/(3x + 19) = x/(3x + 4)`
(x + 3)(3x + 4) = x(3x + 19)
3x2 + 4x + 9x + 12 = 3x2 + 19x
19x – 13x = 12
6x = 12
∴ x = `12/6` = 2
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
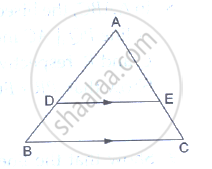
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
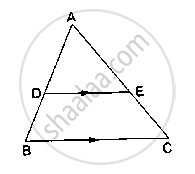
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
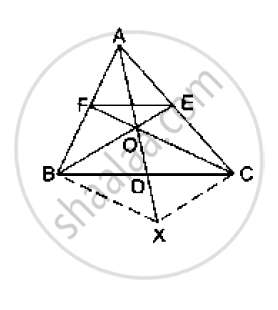
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
Find the height of an equilateral triangle of side 12cm.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

