Advertisements
Advertisements
प्रश्न
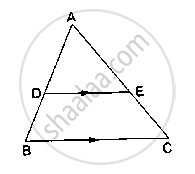
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
उत्तर
In Δ ABC, it is given that DE || BC.
Applying Thales’ Theorem, we get :
`(AD)/(DB) = (AE)/(EC)`
Adding 1 to both sides, we get :
`(AD)/(DB) +1= (AE)/(EC) + 1`
⟹ `(AB)/(DB) = (AC)/(EC)`
⟹ `13.3/(DB) = (11.9)/(5.1)`
⟹ `DB = (13.3 × 5.1)/11.9 =5.7 cm`
Therefore, AD=AB-DB=13.5-5.7=7.6 cm
APPEARS IN
संबंधित प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.
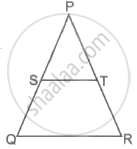
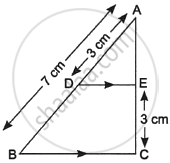
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`