Advertisements
Advertisements
प्रश्न
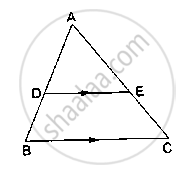
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
उत्तर
In Δ ABC, it is given that DE || BC.
Applying Thales’ theorem, we get :
`(AD)/(DB) = (AE)/(EC)`
⟹ `4/7 =(AE)/(EC)`
Adding 1 to both the sides, we get :
`11/7 = (AC)/(EC)`
⟹ EC = `(6.6 ×7)/11 = 4.2 cm`
Therefore
AE = AC – EC = 6.6 – 4.2 = 2.4 cm
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
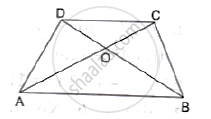
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
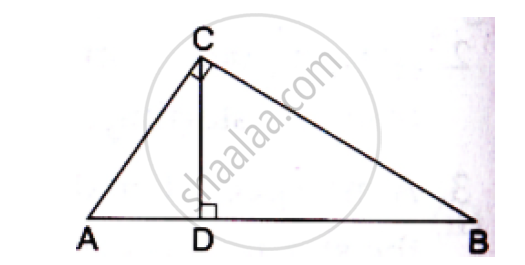
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
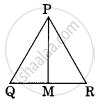
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
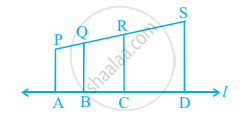
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.