Advertisements
Advertisements
प्रश्न
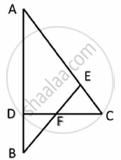
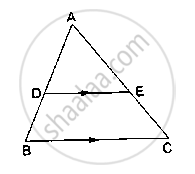
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`
उत्तर
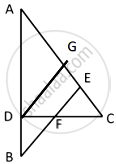
Draw DG || BE
In ΔABE, `(AB)/(BD) = (AE)/(GE)` ...[BPT]
CF = FD [F is the midpoint of DC] ...(i)
In ΔCDG, `(DF)/(CF) = (GE)/(CE)` = 1 ...[Mid point theorem]
GE = CE ...(ii)
∠CEF = ∠CFE ...[Given]
CF = CE [Sides opposite to equal angles] ...(iii)
From (ii) and (iii) CF = GE ...(iv)
From (i) and (iv) GE = FD
∴ `(AB)/(BD) = (AE)/(GE) \implies (AB)/(BD) = (AE)/(FD)`
APPEARS IN
संबंधित प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
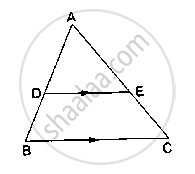
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
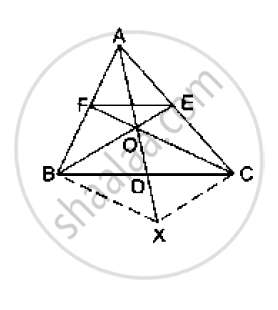
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
State the midpoint theorem
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
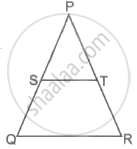
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.