Advertisements
Advertisements
प्रश्न
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`
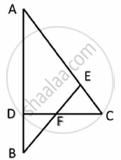
उत्तर
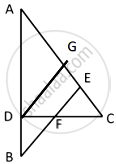
Draw DG || BE
In ΔABE, `(AB)/(BD) = (AE)/(GE)` ...[BPT]
CF = FD [F is the midpoint of DC] ...(i)
In ΔCDG, `(DF)/(CF) = (GE)/(CE)` = 1 ...[Mid point theorem]
GE = CE ...(ii)
∠CEF = ∠CFE ...[Given]
CF = CE [Sides opposite to equal angles] ...(iii)
From (ii) and (iii) CF = GE ...(iv)
From (i) and (iv) GE = FD
∴ `(AB)/(BD) = (AE)/(GE) \implies (AB)/(BD) = (AE)/(FD)`
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
Find the height of an equilateral triangle of side 12cm.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

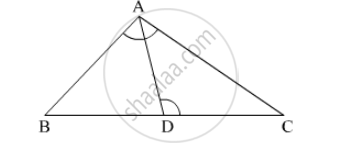
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
