Advertisements
Advertisements
प्रश्न
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
उत्तर

We have, DE || BC
Therefore, by BPT, we have,
`"AD"/"DE"="AE"/"EC"`
`rArr"AD"/"DB"="AE"/"DB"` [∵BD = CE]
⇒ AD = AE
Adding DB on both sides
⇒ AD + DB = AE + DB
⇒ AD + DB = AE + EC [∴ BD = CE]
⇒ AB = AC
⇒ Δ ABC is isosceles
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
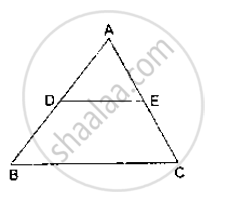
State the basic proportionality theorem.
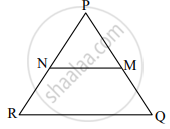
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
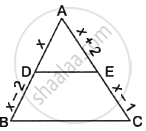
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

