Advertisements
Advertisements
प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
उत्तर
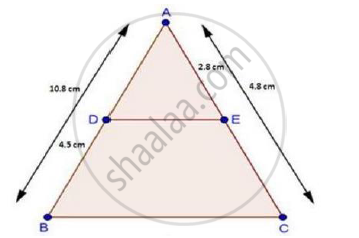
We have,
AB = 10.8cm, BD = 4.5cm, AC = 4.8 cm and AE = 2.8cm
∴ AD = AB – DB = 10.8 – 4.5
⇒ AD = 6.3 cm
And, EC = AC – AE
= 4.8 – 2.8
⇒ EC = 2 cm
Now, `"AD"/"DB"=6.3/4.5=7/5` [∵ AD = 6.3 cm]
And, `"AE"/"EC"=2.8/2=28/20=7/5` [∵ EC = 2 cm]
Thus, DE divides sides AB and AC of ΔABC in the same ratio.
Therefore, by the converse of basic proportionality theorem.
We have, DE || BC
APPEARS IN
संबंधित प्रश्न
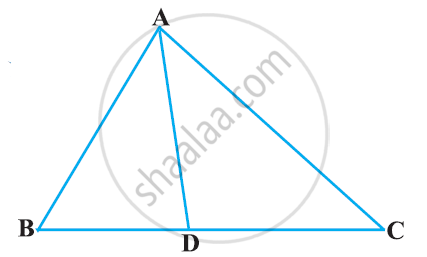
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
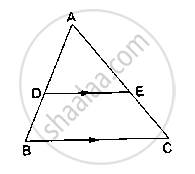
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
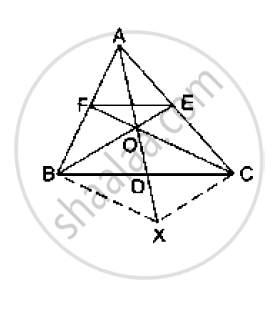
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
