Advertisements
Advertisements
प्रश्न
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
उत्तर
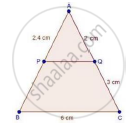
We have || BC
Therefore, by BPT
We have,
`"AP"/"PB"="AQ"/"QC"`
`2.4/"PB"=2/3`
`rArr"PB"=(3xx2.4)/2=(3xx24)/2=(3xx6)/5=18/5`
⇒ PB = 3.6 cm
Now, AB = AP + PB
= 2.4 + 3.6 = 6cm
Now, In ΔAPQ and ΔABC
∠A = ∠A [common]
∠APQ = ∠ABC [∵ PQ || BC ⇒ Corresponding angles are equal]
⇒ ΔAPQ ~ ΔABC [By AA criteria]
`rArr"AB"/"AP"="BC"/"PQ"` [corresponding sides of similar triangles are proportional]
`rArr"PQ"=(6xx2.4)/6`
⇒ PQ = 2.4 cm
Hence, AB = 6 cm and PO = 2.4 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

