Advertisements
Advertisements
प्रश्न
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
उत्तर
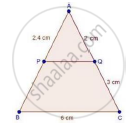
We have || BC
Therefore, by BPT
We have,
`"AP"/"PB"="AQ"/"QC"`
`2.4/"PB"=2/3`
`rArr"PB"=(3xx2.4)/2=(3xx24)/2=(3xx6)/5=18/5`
⇒ PB = 3.6 cm
Now, AB = AP + PB
= 2.4 + 3.6 = 6cm
Now, In ΔAPQ and ΔABC
∠A = ∠A [common]
∠APQ = ∠ABC [∵ PQ || BC ⇒ Corresponding angles are equal]
⇒ ΔAPQ ~ ΔABC [By AA criteria]
`rArr"AB"/"AP"="BC"/"PQ"` [corresponding sides of similar triangles are proportional]
`rArr"PQ"=(6xx2.4)/6`
⇒ PQ = 2.4 cm
Hence, AB = 6 cm and PO = 2.4 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
In a ABC , AD is a median and AL ⊥ BC .
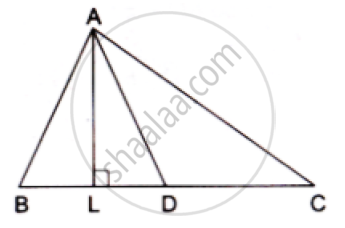
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
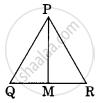
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

