Advertisements
Advertisements
प्रश्न
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

उत्तर
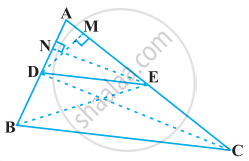
Proof: We are given a triangle ABC in which a line parallel to side BC intersects the other two sides AB and AC at D and E respectively.
We need to prove that `(AD)/(DB) = (AE)/(EC)`
Let us join BE and CD and then draw DM ⊥ AC and EN ⊥ AB.
Now, area of ∆ADE = `1/2` (base × height) = `1/2` AD × EN
The area of ∆ADE is denoted as ar(ADE).
So, ar(ADE) = `1/2` AD × EN
Similarly, ar(BDE) = `1/2` DB × EN,
ar(ADE) = `1/2` AE × DM and ar(DEC) = `1/2` EC × DM
Therefore, `(ar(ADE))/(ar(BDE)) = (1/2 AD xx EN)/(1/2 DB xx EN) = (AD)/(DB)` ......(1)
And `(ar(ADE))/(ar(DEC)) = (1/2 AE xx DM)/(1/2 EC xx DM) = (AE)/(EC)` ......(2)
Note that ∆BDE and DEC are on the same base DE and between the same parallels BC and DE.
So, ar(BDE) = ar(DEC) ......(3)
Therefore, from (1), (2) and (3), we have:
`(AD)/(DB) = (AE)/(EC)`
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
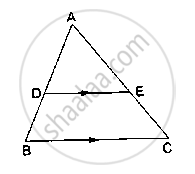
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
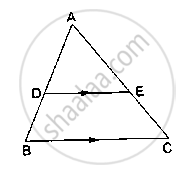
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In a ABC , AD is a median and AL ⊥ BC .
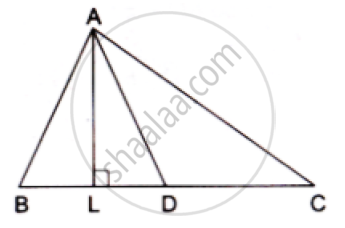
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
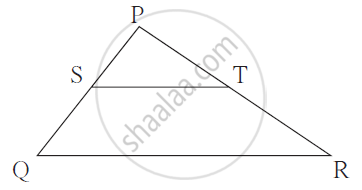
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
