Advertisements
Advertisements
प्रश्न
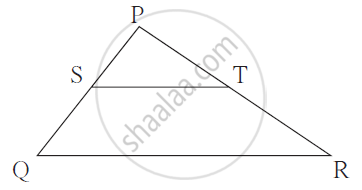
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
उत्तर
In Δ PQR, S and T are midpoints of side PQ and side PR.
ST = 6.2
ST= `1/2` × QR ...............(Theorem of midpoints of two sides of
a triangle.)
`∴6.2 = 1/2`× QR
∴QR = 6.2 × 2
∴QR = 12.4
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In below Fig., state if PQ || EF.
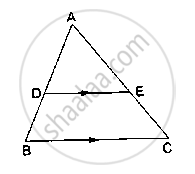
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
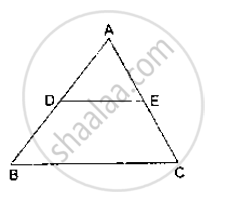
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
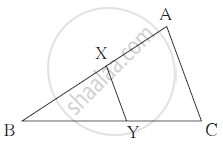
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
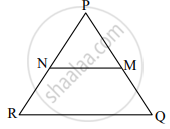
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

