Advertisements
Advertisements
प्रश्न
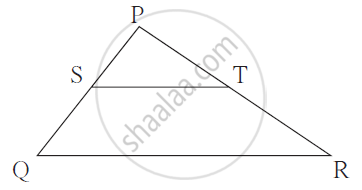
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
उत्तर
In Δ PQR, S and T are midpoints of side PQ and side PR.
ST = 6.2
ST= `1/2` × QR ...............(Theorem of midpoints of two sides of
a triangle.)
`∴6.2 = 1/2`× QR
∴QR = 6.2 × 2
∴QR = 12.4
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
State the midpoint theorem
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
In fig, seg DE || sec BC, identify the correct statement.

A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.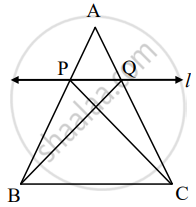
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
