Advertisements
Advertisements
प्रश्न
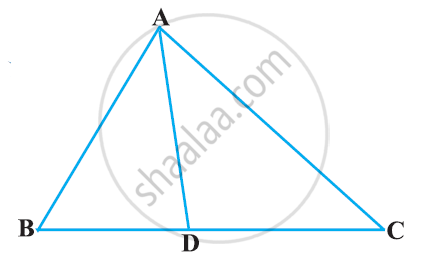
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

उत्तर
Given: ∠𝐴𝐶𝐵 = 90° 𝑎𝑛𝑑 𝐶𝐷 ⊥ 𝐴𝐵
To Prove:` (BC^2)/(AC^2)=(BD)/(AD)`
Proof: In Δ ACB and Δ CDB
∠𝐴𝐶𝐵 = ∠𝐶𝐷𝐵 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐴𝐵𝐶 = ∠𝐶𝐵𝐷 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔCDB
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
`∴ (BC)/(BD)=(AB)/(BC)`
`⇒ BC^2=BD.AB` ..............(1)
In Δ ACB and Δ ADC
∠𝐴𝐶𝐵 = ∠𝐴𝐷𝐶 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐶𝐴𝐵 = ∠𝐷𝐴𝐶 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔADC
When two triangles are similar, then the ratios of their corresponding sides are proportional.
∴ `(AC)/(AD)=(AB)/(AC)`
⇒` AC^2=AD.AB` .................(2)
Dividing (2) by (1), we get
`(BC^2)/(AC^2)=(BD)/(AD)`
APPEARS IN
संबंधित प्रश्न
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
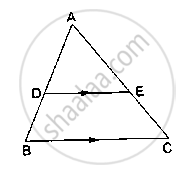
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

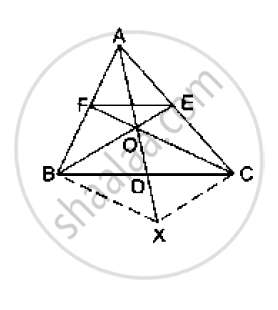
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

State the basic proportionality theorem.
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
