Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

उत्तर
In trapezium ABCD, AB ‖ CD and the diagonals AC and BD intersect at O. Therefore,
`(AO)/(OC)=(BO)/(OD)`
⇒ `(5x-7)/(2x+1)=(7x-5)/(7x+1)`
⟹ (5x-7) (7x+1) = (7x-5) (2x+1)
⟹`35x^2+5x-49x-7=14x^2-10x+7x-5`
⟹ `21x^2-41x-2=0`
⟹`21x^2-42x+x-2=0`
⟹`21x(x-2)+1(x-2)=0`
⟹`(x-2) (2x+1)=0`
⟹ `x=2,1/21`
∵ `x ≠-1/21`
∴ x=2
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
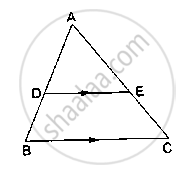
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
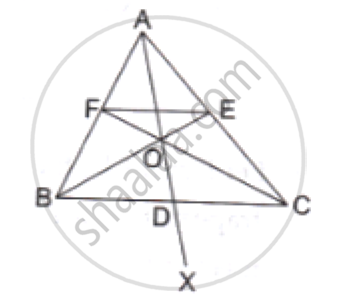
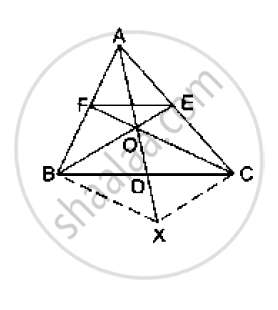
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
State and converse of Thale’s theorem.
