Advertisements
Advertisements
प्रश्न
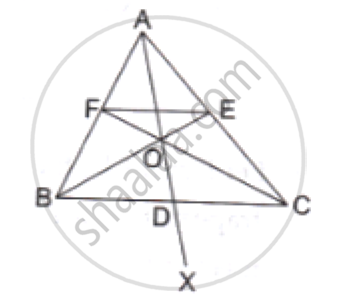
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
उत्तर
In Δ CAB, PQ || AB.
Applying Thales' theorem, we get:
`(CP)/(PB)=(CQ)/(QA)` ...............(1)
Similarly, applying Thales theorem in BDC , Where PR||DM we get:
`(CP)/(PB)=(CR)/(RD)` ..................(2)
Hence, from (1) and (2), we have :
`(CQ)/(QA)=(CR)/(RD)`
Applying the converse of Thales’ theorem, we conclude that QR ‖ AD in Δ ADC. This completes the proof.
APPEARS IN
संबंधित प्रश्न
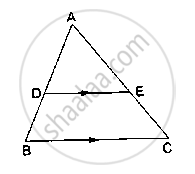
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
