Advertisements
Advertisements
Question
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
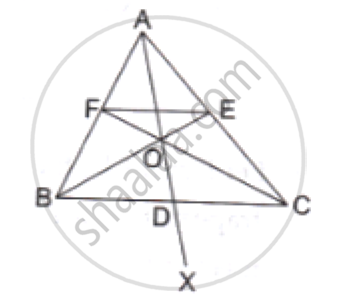
Solution
In Δ CAB, PQ || AB.
Applying Thales' theorem, we get:
`(CP)/(PB)=(CQ)/(QA)` ...............(1)
Similarly, applying Thales theorem in BDC , Where PR||DM we get:
`(CP)/(PB)=(CR)/(RD)` ..................(2)
Hence, from (1) and (2), we have :
`(CQ)/(QA)=(CR)/(RD)`
Applying the converse of Thales’ theorem, we conclude that QR ‖ AD in Δ ADC. This completes the proof.
APPEARS IN
RELATED QUESTIONS
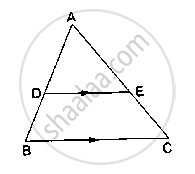
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
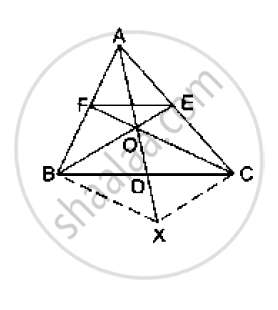
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Find the height of an equilateral triangle of side 12cm.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
