Advertisements
Advertisements
Question
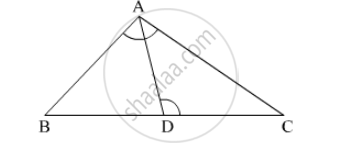
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

Solution
Given: ∠𝐴𝐶𝐵 = 90° 𝑎𝑛𝑑 𝐶𝐷 ⊥ 𝐴𝐵
To Prove:` (BC^2)/(AC^2)=(BD)/(AD)`
Proof: In Δ ACB and Δ CDB
∠𝐴𝐶𝐵 = ∠𝐶𝐷𝐵 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐴𝐵𝐶 = ∠𝐶𝐵𝐷 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔCDB
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
`∴ (BC)/(BD)=(AB)/(BC)`
`⇒ BC^2=BD.AB` ..............(1)
In Δ ACB and Δ ADC
∠𝐴𝐶𝐵 = ∠𝐴𝐷𝐶 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐶𝐴𝐵 = ∠𝐷𝐴𝐶 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔADC
When two triangles are similar, then the ratios of their corresponding sides are proportional.
∴ `(AC)/(AD)=(AB)/(AC)`
⇒` AC^2=AD.AB` .................(2)
Dividing (2) by (1), we get
`(BC^2)/(AC^2)=(BD)/(AD)`
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
