Advertisements
Advertisements
Question
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

Solution
(1)In right-angled triangle AEC, applying Pythagoras theorem, we have:
`AC^2=AE^2+EC^2`
⇒ `B^2=h^2(x+a/2)^2=h^2+x^2+a^2/4+ax`.......(1)
In right – angled triangle AED, we have:
`AD^2=AE^2+ED^2`
⇒ `p^2=h^2+x^2` .............(2)
Therefore,
from (i) and (ii),
`b^2=p^2+ax+a^2/x`
(2) In right-angled triangle AEB, applying Pythagoras, we have:
`AB^2=AE^2+EB^2`
⇒ `c^2=h^2+(a/2-x)^2 (∵ BD=a/2 and BE=BD-x)`
⇒ `C^2=h^2+x^2-a^2/4 (∵ h^2+x^2=p^2)`
⇒`c^2=p^2-ax+a^2/x`
(3)
Adding (i) and (ii), we get:
⇒` b^2+c^2=p^2+ax+a^2/4+p^2-ax+a^2/4`
`=2p^2+ax-ax+(a^2+a^2)/4`
=`2p^2+a^2/2`
(4)
Subtracting (ii) from (i), we get:
`b^2-c^2=p^2+ax+a^2/4-(p^2-ax+a^2/4)`
`=p^2-p^2+ax+ax+a^2/4-a^2/4`
`=2ax`
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 6 cm, DB = 9 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
State the midpoint theorem
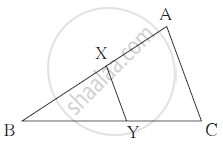
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.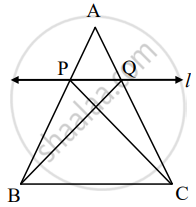
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
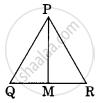
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
