Advertisements
Advertisements
Question
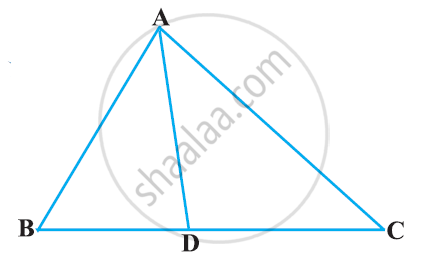
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 6 cm, DB = 9 cm and AE = 8 cm, find AC.
Solution
We have,
DE || BC
Therefore, by basic proportionally theorem,
We have
`"AD"/"DB"="AE"/"EC"`
`rArr6/9=8/"EC"`
`rArr2/3=8/"EC"`
`rArr"EC"=(8xx3)/2`
⇒ EC = 12 cm
⇒ Now, AC = AE + EC = 8 + 12 = 20 cm
∴ AC = 20 cm
APPEARS IN
RELATED QUESTIONS
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

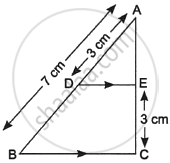
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.