Advertisements
Advertisements
Question
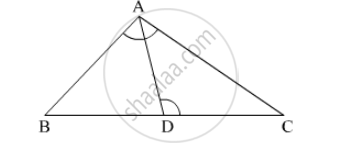
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
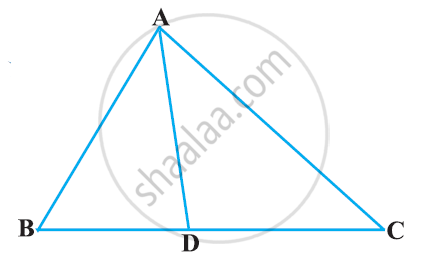
Solution
Let us extend BA to P such that AP = AC. Join PC.
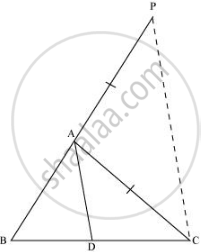
It is given that,
(BD)/(CD) = (AB)/(AC)
=> "BD"/"CD" = "AP"/"AC"
By using the converse of basic proportionality theorem, we obtain
AD || PC
⇒ ∠BAD = ∠APC (Corresponding angles) … (1)
And, ∠DAC = ∠ACP (Alternate interior angles) … (2)
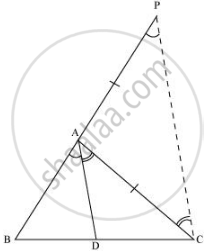
By construction, we have
AP = AC
⇒ ∠APC = ∠ACP … (3)
On comparing equations (1), (2), and (3), we obtain
∠BAD = ∠APC
⇒ AD is the bisector of the angle BAC.
APPEARS IN
RELATED QUESTIONS
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
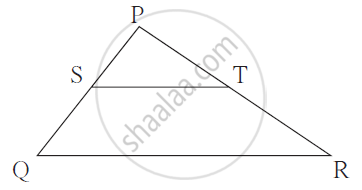
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
In fig, seg DE || sec BC, identify the correct statement.

ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
