Advertisements
Advertisements
Question
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
Solution
Draw AE⊥BC, meeting BC at D.
Applying Pythagoras theorem in right-angled triangle AED, we get:
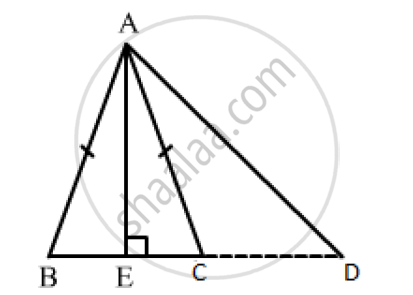
Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.
So, BE = CE
And DE+CE=DE+BE=BD
`AD^2=AE^2+DE^2`
`⇒ AE^2=AD^2-DE^2 ` ...............(1)
In ΔACE,
`AC^2=AE^2+EC^2`
⇒ `AE^2=AC^2-EC^2 ` ...............(2)
Using (i) and (ii),
⇒` AD^2-DE^2=AC^2-EC^2`
⇒` AD^2-AC^2=DE^2-EC^2`
`=(DE+CE) (DE-CE)`
`(DE+BE) CD`
`BD.CD`
APPEARS IN
RELATED QUESTIONS
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
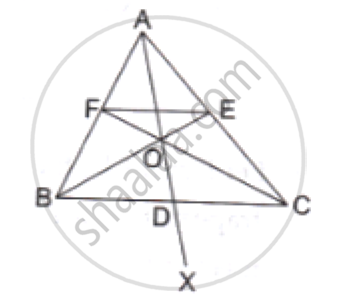
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
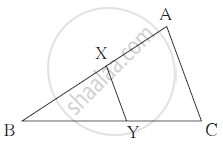
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

