Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
उत्तर
We have, DE || BC
Therefore, by basic proportionality theorem,
We have,
`"AD"/"DB"="AE"/"EC"`
`rArr(4x-3)/(3x-1)=(8x-7)/(5x-3)`
⇒ (4x − 3)(5x − 3) = (8x − 7)(3x − 1)
⇒ 4x(5x − 3) − 3(5x − 3) = 8x(3x − 1) − 7(3x − 1)
⇒ 20x2 − 12x − 15x + 9 = 24x2 − 8x − 21x + 7
⇒ 4x2 − 2x − 2 = 0
⇒ 2(2x2 − x − 1)= 0
⇒ 2x2 − x − 1 = 0
⇒ 2x2 − 2x + 1x − 1 = 0
⇒ 2x(x − 1) + 1(x − 1) = 0
⇒ (2x + 1) (x – 1) = 0
⇒ 2x + 1 = 0 or x – 1 = 0
⇒ x = −1/2 or x = 1
x = −1/2 is not possible
∴ x = 1
APPEARS IN
संबंधित प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
State the basic proportionality theorem.
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
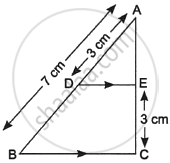
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.