Advertisements
Advertisements
प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

उत्तर
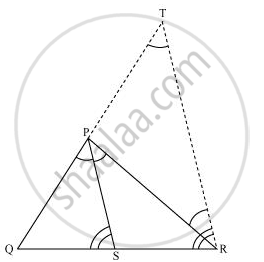
Let us draw a line segment RT parallel to SP which intersects extended line segment QP at point T.
Given that, PS is the angle bisector of ∠QPR.
∠QPS = ∠SPR … (1)
By construction,
∠SPR = ∠PRT (As PS || TR) … (2)
∠QPS = ∠QTR (As PS || TR) … (3)
Using these equations, we obtain
∠PRT = ∠QTR
∴ PT = PR
By construction,
PS || TR
By using basic proportionality theorem for ΔQTR,
`(QS)/(SR) = (QP)/(PT)`
`=>(QS)/(SR) = (PQ)/(PR) (∵ PT = PR)`
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
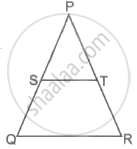
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.