Advertisements
Advertisements
प्रश्न
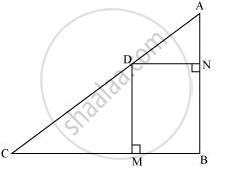
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
उत्तर
(i)Let us join DB.
We have, DN || CB, DM || AB, and ∠B = 90°
∴ DMBN is a rectangle.
∴ DN = MB and DM = NB
The condition to be proved is the case when D is the foot of the perpendicular drawn from B to AC.
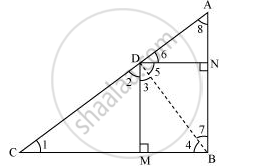
∴ ∠CDB = 90°
⇒ ∠2 + ∠3 = 90° … (1)
In ΔCDM,
∠1 + ∠2 + ∠DMC = 180°
⇒ ∠1 + ∠2 = 90° … (2)
In ΔDMB,
∠3 + ∠DMB + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° … (3)
From equation (1) and (2), we obtain
∠1 = ∠3
From equation (1) and (3), we obtain
∠2 = ∠4
In ΔDCM and ΔBDM,
∠1 = ∠3 (Proved above)
∠2 = ∠4 (Proved above)
∴ ΔDCM ∼ ΔBDM (AA similarity criterion)
=> (BM)/(DM) = (DM)/(MC)
=> (DN)/(DM) = (DM)/(MC) (BM = DN)
⇒ DM2 = DN × MC
(ii) In right triangle DBN,
∠5 + ∠7 = 90° … (4)
In right triangle DAN,
∠6 + ∠8 = 90° … (5)
D is the foot of the perpendicular drawn from B to AC.
∴ ∠ADB = 90°
⇒ ∠5 + ∠6 = 90° … (6)
From equation (4) and (6), we obtain
∠6 = ∠7
From equation (5) and (6), we obtain
∠8 = ∠5
In ΔDNA and ΔBND,
∠6 = ∠7 (Proved above)
∠8 = ∠5 (Proved above)
∴ ΔDNA ∼ ΔBND (AA similarity criterion)
=> AN/DN = DN/NB
⇒ DN2 = AN × NB
⇒ DN2 = AN × DM (As NB = DM)
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

In the given figure MN|| BC and AM: MB= 1: 2
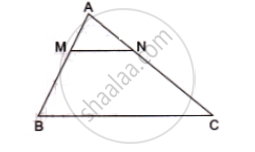
find ` (area(ΔAMN))/(area(ΔABC))`
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

If ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal ______.
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
