Advertisements
Advertisements
Question
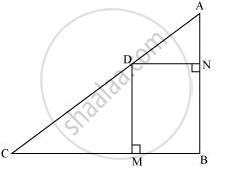
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
Solution
(i)Let us join DB.
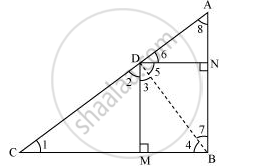
We have, DN || CB, DM || AB, and ∠B = 90°
∴ DMBN is a rectangle.
∴ DN = MB and DM = NB
The condition to be proved is the case when D is the foot of the perpendicular drawn from B to AC.
∴ ∠CDB = 90°
⇒ ∠2 + ∠3 = 90° … (1)
In ΔCDM,
∠1 + ∠2 + ∠DMC = 180°
⇒ ∠1 + ∠2 = 90° … (2)
In ΔDMB,
∠3 + ∠DMB + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° … (3)
From equation (1) and (2), we obtain
∠1 = ∠3
From equation (1) and (3), we obtain
∠2 = ∠4
In ΔDCM and ΔBDM,
∠1 = ∠3 (Proved above)
∠2 = ∠4 (Proved above)
∴ ΔDCM ∼ ΔBDM (AA similarity criterion)
=> (BM)/(DM) = (DM)/(MC)
=> (DN)/(DM) = (DM)/(MC) (BM = DN)
⇒ DM2 = DN × MC
(ii) In right triangle DBN,
∠5 + ∠7 = 90° … (4)
In right triangle DAN,
∠6 + ∠8 = 90° … (5)
D is the foot of the perpendicular drawn from B to AC.
∴ ∠ADB = 90°
⇒ ∠5 + ∠6 = 90° … (6)
From equation (4) and (6), we obtain
∠6 = ∠7
From equation (5) and (6), we obtain
∠8 = ∠5
In ΔDNA and ΔBND,
∠6 = ∠7 (Proved above)
∠8 = ∠5 (Proved above)
∴ ΔDNA ∼ ΔBND (AA similarity criterion)
=> AN/DN = DN/NB
⇒ DN2 = AN × NB
⇒ DN2 = AN × DM (As NB = DM)
APPEARS IN
RELATED QUESTIONS
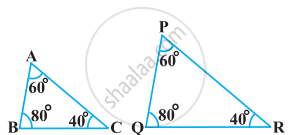
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
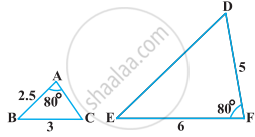
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.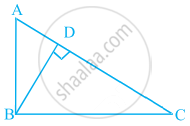
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
