Advertisements
Advertisements
प्रश्न
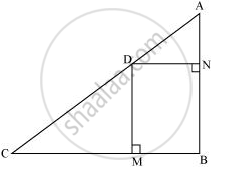
In the given figure, D is a point on hypotenuse AC of ΔABC, DM ⊥ BC and DN ⊥ AB, Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
उत्तर
(i)Let us join DB.
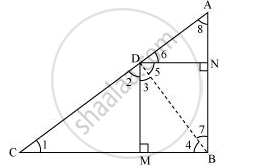
We have, DN || CB, DM || AB, and ∠B = 90°
∴ DMBN is a rectangle.
∴ DN = MB and DM = NB
The condition to be proved is the case when D is the foot of the perpendicular drawn from B to AC.
∴ ∠CDB = 90°
⇒ ∠2 + ∠3 = 90° … (1)
In ΔCDM,
∠1 + ∠2 + ∠DMC = 180°
⇒ ∠1 + ∠2 = 90° … (2)
In ΔDMB,
∠3 + ∠DMB + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° … (3)
From equation (1) and (2), we obtain
∠1 = ∠3
From equation (1) and (3), we obtain
∠2 = ∠4
In ΔDCM and ΔBDM,
∠1 = ∠3 (Proved above)
∠2 = ∠4 (Proved above)
∴ ΔDCM ∼ ΔBDM (AA similarity criterion)
=> (BM)/(DM) = (DM)/(MC)
=> (DN)/(DM) = (DM)/(MC) (BM = DN)
⇒ DM2 = DN × MC
(ii) In right triangle DBN,
∠5 + ∠7 = 90° … (4)
In right triangle DAN,
∠6 + ∠8 = 90° … (5)
D is the foot of the perpendicular drawn from B to AC.
∴ ∠ADB = 90°
⇒ ∠5 + ∠6 = 90° … (6)
From equation (4) and (6), we obtain
∠6 = ∠7
From equation (5) and (6), we obtain
∠8 = ∠5
In ΔDNA and ΔBND,
∠6 = ∠7 (Proved above)
∠8 = ∠5 (Proved above)
∴ ΔDNA ∼ ΔBND (AA similarity criterion)
=> AN/DN = DN/NB
⇒ DN2 = AN × NB
⇒ DN2 = AN × DM (As NB = DM)
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
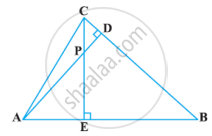
ΔABD ∼ ΔCBE
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
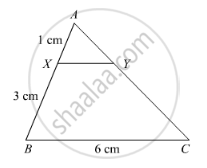
In the following figure, XY || BC. Find the length of XY.
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.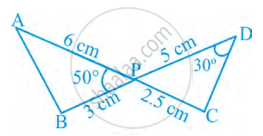
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
